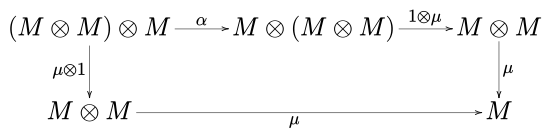Monoid (teori kategori)
Dalam teori kategori, cabang dari matematika, monoid (atau benda monoid) (M, μ, η) dalam kategori monoidal (C, ⊗, I) adalah objek M bersama dengan dua morfisme
- μ: M ⊗ M → M disebut perkalian,
- η: I → M adalah unit,
sedemikian rupa sehingga segi lima diagram
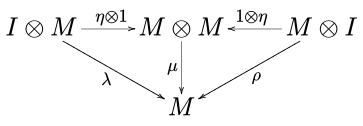
dan diagram unitor
Gambar di atas adalah sifat komutatif. Dalam notasi di atas, I adalah elemen satuan dan α, λ dan ρ adalah asosiatif, identitas kiri dan identitas kanan dari kategori monoid C.
Monoid yang lain, komonoid dalam kategori monoid C adalah monoid dalam kategori ganda Cop.
Misal, kategori monoidal C memiliki simetri γ. Monoid M dalam C adalah sifat komutatif dengan μ o γ = μ.
Contoh
sunting- Sebuah objek monoid dalam Himpunan, kategori himpunan (dengan struktur monoid induksi dari produk Kartesius), adalah monoid dalam arti biasa.
- Objek monoid di Atas dengan kategori ruang topologi (dengan struktur monoid induksi dari topologi produk), adalah monoid topologi.
- Objek monoid dalam kategori monoid (dengan produk langsung dari monoid) hanyalah sebuah monoid komutatif. Dengan menggunakan sifat Argumen Eckmann–Hilton.
- Objek monoid dalam kategori semikisi-gabungan kompleks Sup (dengan struktur monoid induksi dari produk Kartesius) adalah kuantale unital.
- Objek monoid (Ab, ⊗Z, Z), kategori grup abelian, adalah gelanggang.
- Untuk gelanggang komutatif R, objek monoid, khusus
- (R-Mod, ⊗R, R), kategori modul di atas R, adalah aljabar-R.
- Kategori modul bertingkat adalah aljabar-R bertingkat.
- kategori kompleks rantai dari modul-R adalah aljabar bertingkat diferensial.
- Objek monoid dalam K -Vekt, kategori ruang vektor-K (dengan hasil kali tensor), adalah aljabar-K, dan objek komonoid adalah koaljabar-K.
- Untuk setiap kategori C, kategori [C, C] dari endofunktor memiliki struktur monoid yang diinduksi oleh komposisi dan identitas funktor IC. Objek monoid [C,C] adalah monad dengan C.
- Untuk kategori dengan produk hingga, setiap objek menjadi objek komonoid melalui morfisme diagonal . Menggandakan dalam kategori dengan koproduk hingga untuk objek menjadi objek monoid dengan .
Kategori monoid
suntingDiberikan dua monoid (M, μ, η) dan (M', μ', η') dalam kategori monoidal C, morfisme f : M → M ' adalah morfisme monoid saat
- f o μ = μ' o (f ⊗ f),
- f o η = η'.
Dengan kata lain, diagram berikut
perjalanan.
Kategori monoid di C dan morfisme monoidnya ditulis MonC.[1]
Lihat pula
sunting- Tindakan-S, kategori monoid yang bekerja pada himpunan
Referensi
sunting- ^ Section VII.3 in Mac Lane, Saunders (1988). Categories for the working mathematician (edisi ke-4th corr. print.). New York: Springer-Verlag. ISBN 0-387-90035-7.
- Mati Kilp, Ulrich Knauer, Alexander V. Mikhalov, Monoids, Acts and Categories (2000), Walter de Gruyter, Berlin ISBN 3-11-015248-7