1 + 2 + 4 + 8 + ⋯

Dalam matematika, 1 + 2 + 4 + 8 + ⋯ adalah deret tak terhingga yang suku-sukunya berupa pangkat dua. Sebagai deret geometrik, deret ini mempunyai suku pertama, 1, dan rasio umum, 2. Sebagai deret bilangan riil, deret ini divergen menuju ke tak terhingga, dalam artian tidak memiliki penjumlahan. Dalam arti yang lebih luas, deret ini dikaitkan dengan nilai selain $\infty$ , yaitu −1, yang merupakan batas deret menggunakan metrik 2-adic.

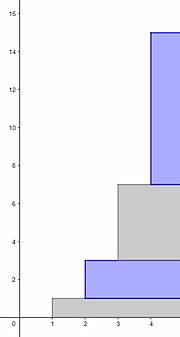
Penjumlahan

Jumlah parsial $1+2+4+8+\cdots$ adalah $1,3,7,15,\dots$ karena deret tersebut divergen menuju ke tak terhingga. Begitu pula dengan deret.

2^{0}+2^{1}+\cdots +2^{k}=2^{k+1}-1

Oleh karena itu, setiap metode penjumlahan beraturan total memberikan nilai penjumlahan, yaitu tak terhingga. Contoh metode tersebut di antaranya penjumlahan Cesàro dan penjumlahan Abel.^[1] Di sisi lain, setidaknya ada satu metode yang secara umum berguna yang menghitung penjumlahan $1+2+4+8+\cdots$ , dan hasil penjumlahan tersebut memberikan nilai terhingga, yaitu −1. Deret pangkat iring $f(x)=1+2x+4x^{2}+8x^{3}+\cdots +2^{n}{}x^{n}+\cdots ={\frac {1}{1-2x}}$ memiliki jeruji kekonvergenan di antara 0 dan 1 2, sehingga tidak konvergen di $x=1$ . Meskipun demikian, fungsi $f$ yang terdefinisi memiliki kekontinuan analitik tunggal untuk bidang kompleks dengan menghilangkan titik ${\textstyle x={\frac {1}{2}}}$ , dan deret ini dirumuskan dengan aturan yang sama, yaitu ${\textstyle f(x)={\frac {1}{1-2x}}}$ . Karena $f(1)=-1$ , maka deret aslinya $1+2+4+8+\dots$ dikatakan terjumlahkan (E) menjadi −1, dan −1 merupakan jumlah (E) dari deret tersebut. (Notasi ini dipakai oleh G. H. Hardy untuk mengartikan pendekatan Euler menuju deret divergen).^[2]

Pendekatan yang hampir identik (yang dikerjakan oleh Euler sendiri) adalah dengan memisalkan deret pangkat yang semua koefisiennya adalah 1, yaitu $1+y+y^{2}+y^{3}+\cdots ={\frac {1}{1-y}}$ dan memasukkan $y=2$ . Dengan demikian, kedua deret di atas berkaitan dengan substitusi $y=2x$ .

Fakta bahwa penjumlahan (E) yang memberikan nilai terhingga $1+2+4+8+\cdots$ menunjukkan bahwa metode umum tidak beraturan sepenuhnya. Di sisi lain, penjumlahan (E) memiliki beberapa sifat lain yang diinginkan untuk metode penjumlahan, di antaranya stabilitas dan linieritas. Dua aksioma terakhir ini sebenarnya memaksa penjumlahan bernilai menjadi −1, dengan memanipulasi aljabar berikut:

{\begin{array}{rcl}s&=&\displaystyle 1+2+4+8+16+\cdots \\&=&\displaystyle 1+2(1+2+4+8+\cdots )\\&=&\displaystyle 1+2s\end{array}}

$s=\infty$ merupakan akar persamaan $s=1+2s$ .^[a] Jika terdapat beberapa metode penjumlahan yang mengembalikan bilangan biasa untuk $s$ , yaitu bukan $\infty$ , maka dapat mudah ditentukan perhitungan tersebut. Dalam hal ini, $s$ dapat dikurangi dari kedua ruas persamaan, yang mengakibatkan persamaan menjadi $0=1+s$ , dan demikian bahwa $s=-1$ .^[3]

Manipulasi di atas dapat digunakan untuk menghasilkan −1 di luar konteks dalam mengerjakan penjumlahan yang cukup kuat. Untuk konsep penjumlahan yang paling terkenal dan yang mudah, seperti konsep penjumlahan konvergen fundamental, tidak masuk akal bahwa deret dari suku positif dapat bernilai negatif. Fenomena yang serupa terjadi dengan deret Grandi, sebuah deret divergen dengan jumlah deret dari suku berupa bilangan bulat memiliki hasil yang bukan bilangan bulat, yaitu 12. Contoh-contoh ini mengilustrasikan bahayanya dalam menerapkan argumen serupa ke deret yang tersirat oleh desimal berulang seperti 0,11 ... dan yang paling terkenal, 0,999…. Argumen dibenarkan untuk deret konvergen ini, yang menyiratkan bahwa 0.111… = 19 dan 0.999… = 1, tetapi bukti yang mendasari menuntut pemikiran yang cermat tentang pandangan penjumlahan yang tak berakhir.^[4]

Selain itu, deret $1+2+4+8+\cdots$ juga dapat dipandang sebagai deret yang konvergen dalam sistem bilangan yang berbeda dari bilangan real, yaitu, bilangan 2-adic. Sebagai deret bilangan 2-adic, deret ini konvergen menuju ke hasil jumlah yang sama, −1, yang dapat diperoleh dengan menggunakan kekontinuan analitik.^[5]

Lihat pula

Catatan

^ Sebagai contoh, $\infty$ merupakan simbol yang menyatakan salah satu dari dua titik tetap dari transformasi Möbius $z\to 1+2z$ di bola Riemann.

^ Hardy 1949, hlm. 10.
^ Hardy 1949, hlm. 8, 10.
^ Hardy 1949, hlm. 19, membahas tentang dua akar dari persamaan $s = 1 + 2 s$ .
^ Gardiner 2002, hlm. 93–99, Di hlm. 95, terdapat argumen bahwa $1 + 2 + 4 + 8 + \dots$ agak sedikit berbeda, tetapi konsepnya sama.
^ Koblitz, Neal (1984). p-adic Numbers, p-adic Analysis, and Zeta-Functions. Graduate Texts in Mathematics, vol. 58. Springer-Verlag. hlm. 20. ISBN 0-387-96017-1.

Referensi

Euler, Leonhard (1760). "De seriebus divergentibus". Novi Commentarii academiae scientiarum Petropolitanae. 5: 205–237.
Gardiner, A. (2002) [1982]. Understanding infinity: the mathematics of infinite processes (edisi ke-Dover). Dover. ISBN 0-486-42538-X.
Hardy, G. H. (1949). Divergent Series. Clarendon Press. LCC QA295 .H29 1967.

Bacaan lebih lanjut

Barbeau, E. J.; Leah, P. J. (May 1976). "Euler's 1760 paper on divergent series". Historia Mathematica. 3 (2): 141–160. doi:10.1016/0315-0860(76)90030-6.
Ferraro, Giovanni (2002). "Convergence and Formal Manipulation of Series from the Origins of Calculus to About 1730". Annals of Science. 59: 179–199. doi:10.1080/00033790010028179.
Kline, Morris (November 1983). "Euler and Infinite Series". Mathematics Magazine. 56 (5): 307–314. doi:10.2307/2690371. JSTOR 2690371.
Sandifer, Ed (June 2006). "Divergent series" (PDF). How Euler Did It. MAA Online. Diarsipkan dari versi asli (PDF) tanggal 2013-03-20. Diakses tanggal 2020-09-24.
Sierpińska, Anna (November 1987). "Humanities students and epistemological obstacles related to limits". Educational Studies in Mathematics. 18 (4): 371–396. doi:10.1007/BF00240986. JSTOR 3482354.

[3] Sebagai contoh, $\infty$ merupakan simbol yang menyatakan salah satu dari dua titik tetap dari transformasi Möbius $z\to 1+2z$ di bola Riemann.

[FOOTNOTEHardy194910-1] Hardy 1949, hlm. 10.

[FOOTNOTEHardy19498,_10-2] Hardy 1949, hlm. 8, 10.

[FOOTNOTEHardy194919membahas_tentang_dua_akar_dari_persamaan_<span_class="texhtml"_style="white-space:_nowrap;">''s''_=_1_+_2''s''</span>-4] Hardy 1949, hlm. 19, membahas tentang dua akar dari persamaan $s = 1 + 2 s$ .

[FOOTNOTEGardiner200293–99Di_hlm._95,_terdapat_argumen_bahwa_<span_class="texhtml"_style="white-space:_nowrap;">1_+_2_+_4_+_8_+_⋯</span>_agak_sedikit_berbeda,_tetapi_konsepnya_sama-5] Gardiner 2002, hlm. 93–99, Di hlm. 95, terdapat argumen bahwa $1 + 2 + 4 + 8 + \dots$ agak sedikit berbeda, tetapi konsepnya sama.

[6] Koblitz, Neal (1984). p-adic Numbers, p-adic Analysis, and Zeta-Functions. Graduate Texts in Mathematics, vol. 58. Springer-Verlag. hlm. 20. ISBN 0-387-96017-1.

[1]

[2]

[a]

[3]

[4]

[5]