Titik pencil
Dalam matematika, sebuah titik x dinamakan titik pencil dari himpunan bagian S (dalam ruang topologi X) bila x adalah elemen S,namun ada persekitaran x yang tidak mengandung titik-titik lain mana pun dari S. Bila ruang X adalah ruang Euklides atau ruang metrik lainnya, maka x adalah titik pencil S bila ada bola terbuka di sekitar x yang tidak berisikan titik-titik lain mana pun dari S. (Dengan memperkenalkan konsep barisan dan limit, kita dapat menyebutkan secara ekivalen bahwa titik x adalah titik pencil dari S jika dan hanya cika titik itu bukan titik batas dari S.)
Himpunan yang hanya terdiri dari titik-titik pencil dinamakan himpunan diskret. Himpunan bagian S dari ruang Euklides haruslah tercacahkan, karena pemencilan tiap-tiap titik, ditambah pula dengan fakta bahwa bilangan rasional adalah rapat dalam bilangan riil, ini berarti bahwa titik-titik dari S dapat dipetakan ke dalam himpunan titik-titik dengan koordinat rasional, yang jumlahnya tercacahkan. Namun tidak setiap himpunan tercacahkan adalah diskret. Bilangan rasional dalam ruang metrik Euklides adalah contoh yang umum.
Himpunan tertutup tanpa titik pencil dinamakan himpunan sempurna (semua titik batas berada di dalamnya, dan tidak ada titik yang terpencil dari himpunan itu).
Contoh-contoh standar
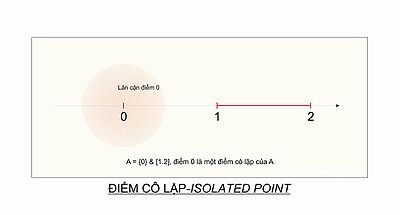
sunting- Untuk himpunan , titik 0 adalah titik pencil
- Untuk himpunan , tiap titik 1/k adalah titik pencil, namun 0 bukan titik pencil karena ada titik lain dalam S yang bisa dibuat sedekat mungkin dengan 0.
- Himpunan dari bilangan asli adalah himpunan diskret.
Lihat pula
suntingReferensi
sunting- Gomez-Ramirez, Danny (2007), "An explicit set of isolated points in R with uncountable closure", Matemáticas: Enseñanza universitaria, Escuela Regional de Matemáticas. Universidad del Valle, Colombia, 15: 145–147
Pranala luar
sunting- (Inggris) Weisstein, Eric W. "Isolated Point". MathWorld.