Wikipedia

Bilangan prima terbesar yang diketahui

(Dialihkan dari Bilangan prima terbesar)

Bilangan prima terbesar yang diketahui (hingga September 2021) adalah 282,589,933 − 1, sebuah bilangan dengan 24,862,048 digit ketika ditulis dalam basis desimal. Bilangan ini temukan lewat komputer yang disumbangkan secara sukarela oleh Patrick Laroche dari Great Internet Mersenne Prime Search (GIMPS) pada tahun 2018.

Plot banyaknya digit pada bilangan prima terbesar yang diketahui per tahun, sejak kemunculan komputer elektronik. Sumbu vertikal memakai skala logaritma.

Bilangan prima adalah bilangan bulat positif, selain angka 1, yang tidak memiliki faktor selain angka 1 dan dirinya sendiri. Teorema Euklides menyatakan ada tak hingga banyaknya bilangan prima, sehingga tidak ada bilangan prima terbesar.

Banyak bilangan prima terbesar yang diketahui merupakan prima Mersenne karena ada tes bilangan prima yang lebih cepat untuk bilangan prima jenis ini daripada tes pada umumnya. Bilangan prima ini berbentuk 2k − 1, yang dalam bentuk binernya berupa k digit angka 1.[1] Hingga Desember 2020, delapan bilangan prima terbesar merupakan prima Mersenne.[2] Tujuh belas rekor prima terbesar terakhir berbentuk prima Mersenne.[3][4]

Implementasi transformasi Fourier cepat dari tes bilangan prima Lucas-Lehmer untuk bilangan Mersenne menghasilkan tes bilangan prima yang sangat cepat jika dibandingkan dengan tes bilangan prima lain yang dikenal untuk jenis-jenis bilangan yang lain. Dengan komputer saat ini, jutaan digit bilangan mirip-Mersenne dapat dibuktikan merupakan bilangan prima, namun hanya ribuan digit bilangan [jenis] lain yang dapat dibuktikan merupakan bilangan prima.

Rekor saat ini

sunting

Rekor saat ini adalah bilangan 282,589,933 − 1 dengan 24.862.048 digit, ditemukan oleh GIMPS pada Desember 2018.[5] Nilai 120 digit pertama dan digit terakhir bilangan ini adalah:

148894445742041325547806458472397916603026273992795324185271289425213239361064475310309971132180337174752834401423587560 ...

(24.861.808 digit diabaikan)

... 062107557947958297531595208807192693676521782184472526640076912114355308311969487633766457823695074037951210325217902591[6]

Hadiah

sunting

Great Internet Mersenne Prime Search (GIMPS) saat ini menawarkan US$3.000 untuk peserta yang mengunduh dan menjalankan program gratis mereka dan menemukan bilangan prima yang memiliki kurang dari 100 juta digit.

Terdapat beberapa hadiah yang ditawarkan oleh Electronic Frontier Foundation untuk rekor bilangan prima.[7] GIMPS juga mengkoordinasikan usaha mereka mencari bilangan prima dengan 100 juga digit atau lebih besar, dan akan membagi (split) US$150.000 bersama Electronic Frontier Foundation kepada peserta yang memenangkan rekor. Rekor prima dengan satu juta digit terpecahkan pada tahun 1999, dengan hadiah US$50.000.[8] Pada tahun 2008, rekor melampaui sepuluh juta digit, dengan hadiah US$100.000 dan Cooperative Computing Award dari Electronic Frontier Foundation.[7] Majalah Time menyebutnya sebagai penemuan ke-29 terbaik pada tahun 2008.[9] Kedua hadiah US$50.000 dan US$100.000 dimenangkan oleh peserta GIMPS. Hadiah tambahan ditawarkan untuk bilangan prima terbesar yang ditemukan, yang memiliki setidaknya seratus juta digit dan yang memiliki setidaknya satu miliar digit.[7]

Sejarah

sunting
 
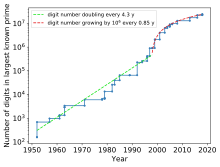
Cap pos peringatan (commemorative) yang digunakan Departemen Matematika UIUC setelah membuktikan M11213 merupakan bilangan prima.

Tabel berikut menyajikan perkembangan bilangan prima terbesar yang diketahui, disusun menaik.[3] Disini, Mp = 2p − 1 adalah bilangan Mersenne dengan eksponen p. Rekor terlama adalah M19 = 524,287, bilangan prima terbesar yang diketahui selama 144 tahun. Tidak ada rekor yang diketahui sebelum tahun 1456.

Bilangan Ekspansi desimal

(hanya untuk bilangan < M1000)

Banyak digit Tahun ditemukan Penemu
M13 8,191 4 1456 Tanpa nama
M17 131,071 6 1588 Pietro Cataldi
M19 524,287 6 1588 Pietro Cataldi
  6,700,417 7 1732 Leonhard Euler(?)

Euler tidak menerbitkan secara eksplisit keprimaan 6,700,417, tapi teknik yang ia gunakan untuk memfaktorkan 232 + 1 mengartikan dia telah mengerjakan sebagian besar bukti yang diperlukan, dan beberapa ahli percaya ia mengetahui keprimaan bilangan ini.[10]

M31 2,147,483,647 10 1772 Leonhard Euler
  999,999,000,001 12 1851 Disertakan (tapi dibubuhi tanda tanya) dalam suatu daftar bilangan prima yang dibuat Looff. Karena ketidakyakinannya, beberapa tidak mengikutkan bilangan ini sebagai rekor.
  67,280,421,310,721 14 1855 Thomas Clausen (tapi tanpa disertai buki).
M127 170,141,183,460,469,231,731,687,303,715,884,105,727 39 1876 Édouard Lucas
  20,988,936,657,440,586,486,151,264,256,610,222,593,863,921 44 1951 Aimé Ferrier dengan kalkulator mekanik; rekor terbesar yang tidak dipecahkan dengan menggunakan komputer.
180×(M127)2+1 5210644015679228794060694325390955853335898483908056458352183851018372555735221 79 1951 J. C. P. Miller dan D. J. Wheeler[11] menggunakan komputer EDSAC Cambridge
M521 6864797660130609714981900799081393217269435300143305409394463459185543183397656052122559640661454554977296311391480858037121987999716643812574028291115057151 157 1952
M607 531137992816767098689588206552468627329593117727031923199444138200403559860852242739162502265229285668889329486246501015346579337652707239409519978766587351943831270835393219031728127 183 1952
M1279 104079321946...703168729087 386 1952
M2203 147597991521...686697771007 664 1952
M2281 446087557183...418132836351 687 1952
M3217 259117086013...362909315071 969 1957
M4423 285542542228...902608580607 1,332 1961
M9689 478220278805...826225754111 2,917 1963
M9941 346088282490...883789463551 2,993 1963
M11213 281411201369...087696392191 3,376 1963
M19937 431542479738...030968041471 6,002 1971 Bryant Tuckerman
M21701 448679166119...353511882751 6,533 1978 Laura A. Nickel dan Landon Curt Noll[12]
M23209 402874115778...523779264511 6,987 1979 Landon Curt Noll[12]
M44497 854509824303...961011228671 13,395 1979 David Slowinski dan Harry L. Nelson[12]
M86243 536927995502...709433438207 25,962 1982 David Slowinski[12]
M132049 512740276269...455730061311 39,751 1983 David Slowinski[12]
M216091 746093103064...103815528447 65,050 1985 David Slowinski[12]
  148140632376...836387377151 65,087 1989 Sebuah grup bernama "Amdahl Six": John Brown, Landon Curt Noll, B. K. Parady, Gene Ward Smith, Joel F. Smith, Sergio E. Zarantonello.[13][14] Ini adalah bilangan prima bukan-Mersenne terbesar yang diketahui ketika ditemukan.
M756839 174135906820...328544677887 227,832 1992 David Slowinski dan Paul Gage[12]
M859433 129498125604...243500142591 258,716 1994 David Slowinski dan Paul Gage[12]
M1257787 412245773621...976089366527 378,632 1996 David Slowinski dan Paul Gage[12]
M1398269 814717564412...868451315711 420,921 1996 GIMPS, Joel Armengaud
M2976221 623340076248...743729201151 895,932 1997 GIMPS, Gordon Spence
M3021377 127411683030...973024694271 909,526 1998 GIMPS, Roland Clarkson
M6972593 437075744127...142924193791 2,098,960 1999 GIMPS, Nayan Hajratwala
M13466917 924947738006...470256259071 4,053,946 2001 GIMPS, Michael Cameron
M20996011 125976895450...762855682047 6,320,430 2003 GIMPS, Michael Shafer
M24036583 299410429404...882733969407 7,235,733 2004 GIMPS, Josh Findley
M25964951 122164630061...280577077247 7,816,230 2005 GIMPS, Martin Nowak
M30402457 315416475618...411652943871 9,152,052 2005 GIMPS, Curtis Cooper dan Steven Boone
M32582657 124575026015...154053967871 9,808,358 2006 GIMPS, Curtis Cooper dan Steven Boone
M43112609 316470269330...166697152511 12,978,189 2008 GIMPS, Edson Smith
M57885161 581887266232...071724285951 17,425,170 2013 GIMPS, Curtis Cooper
M74207281 300376418084...391086436351 22,338,618 2016 GIMPS, Curtis Cooper
M77232917 467333183359...069762179071 23,249,425 2017 GIMPS, Jonathan Pace
M82589933 148894445742...325217902591 24,862,048 2018 GIMPS, Patrick Laroche

GIMPS mendapati lima belas rekor terakhir (semuanya berupa bilangan Mersenne) ditemukan dengan komputer biasa yang dioperasikan oleh peserta-peserta di seluruh dunia.

Dua puluh bilangan prima terbesar

sunting

Sebuah daftar 5.000 bilangan prima terbesar diurus oleh by Chris K. Caldwell;[15][16] dua puluh bilangan terbesarnya disajikan pada tabel berikut.

Peringkat Bilangan Tanggal penemua Banyak digit Jenis bilangan Referensi
1 282589933 − 1 2018-12-07 24,862,048 Mersenne [5]
2 277232917 − 1 2017-12-26 23,249,425 Mersenne [17]
3 274207281 − 1 2016-01-07 22,338,618 Mersenne [18]
4 257885161 − 1 2013-01-25 17,425,170 Mersenne [19]
5 243112609 − 1 2008-08-23 12,978,189 Mersenne [20]
6 242643801 − 1 2009-06-04 12,837,064 Mersenne [21]
7 237156667 − 1 2008-09-06 11,185,272 Mersenne [20]
8 232582657 − 1 2006-09-04 9,808,358 Mersenne [22]
9 10223 × 231172165 + 1 2016-10-31 9,383,761 Proth [23]
10 230402457 − 1 2005-12-15 9,152,052 Mersenne [24]
11 225964951 − 1 2005-02-18 7,816,230 Mersenne [25]
12 224036583 − 1 2004-05-15 7,235,733 Mersenne [26]
13 202705 × 221320516 + 1 2021-12-01 6,418,121 Proth
14 220996011 − 1 2003-11-17 6,320,430 Mersenne [27]
15 10590941048576 + 1 2018-10-31 6,317,602 Fermat yang diperumum [28]
16 9194441048576 + 1 2017-08-29 6,253,210 Fermat yang diperumum [29]
17 168451 × 219375200 + 1 2017-09-17 5,832,522 Proth [30]
18 69 × 218831865 − 1 2021-12-16 5,668,959
19 7 × 218233956 + 1 2020-10-01 5,488,969 Proth [31]
20 3  ×  217748034 − 1 2021-09-06 5,342,692 321 [32]

Referensi

sunting
  1. ^ "Perfect Numbers". Penn State University. Diakses tanggal 6 October 2019. An interesting side note is about the binary representations of those numbers... 
  2. ^ Caldwell, Chris. "The largest known primes – Database Search Output". Prime Pages. Diakses tanggal June 3, 2018. 
  3. ^ a b Caldwell, Chris. "The Largest Known Prime by Year: A Brief History". Prime Pages. Diakses tanggal January 20, 2016. 
  4. ^ The last non-Mersenne to be the largest known prime, was 391,581 ⋅ 2216,193 − 1; see also The Largest Known Prime by year: A Brief History by Caldwell.
  5. ^ a b "GIMPS Project Discovers Largest Known Prime Number: 282,589,933-1". Mersenne Research, Inc. 21 December 2018. Diakses tanggal 21 December 2018.  Kesalahan pengutipan: Tanda <ref> tidak sah; nama "GIMPS-2018" didefinisikan berulang dengan isi berbeda
  6. ^ "51st Known Mersenne Prime Discovered". 
  7. ^ a b c "Record 12-Million-Digit Prime Number Nets $100,000 Prize". Electronic Frontier Foundation. Electronic Frontier Foundation. October 14, 2009. Diakses tanggal November 26, 2011. 
  8. ^ Electronic Frontier Foundation, Big Prime Nets Big Prize.
  9. ^ "Best Inventions of 2008 - 29. The 46th Mersenne Prime". Time. Time Inc. October 29, 2008. Diarsipkan dari versi asli tanggal November 2, 2008. Diakses tanggal January 17, 2012. 
  10. ^ Edward Sandifer, C. (19 November 2014). How Euler Did Even More. ISBN 9780883855843. 
  11. ^ J. Miller, Large Prime Numbers. Nature 168, 838 (1951).
  12. ^ a b c d e f g h i Landon Curt Noll, Large Prime Number Found by SGI/Cray Supercomputer.
  13. ^ Letters to the Editor. The American Mathematical Monthly 97, no. 3 (1990), p. 214. Accessed May 22, 2020.
  14. ^ Proof-code: Z, The Prime Pages.
  15. ^ "The Prime Database: The List of Largest Known Primes Home Page". primes.utm.edu/primes. Chris K. Caldwell. Diakses tanggal 30 September 2017. 
  16. ^ "The Top Twenty: Largest Known Primes". Chris K. Caldwell. Diakses tanggal 3 January 2018. 
  17. ^ "GIMPS Project Discovers Largest Known Prime Number: 277,232,917-1". mersenne.org. Great Internet Mersenne Prime Search. Diakses tanggal 3 January 2018. 
  18. ^ "GIMPS Project Discovers Largest Known Prime Number: 274,207,281-1". mersenne.org. Great Internet Mersenne Prime Search. Diakses tanggal 29 September 2017. 
  19. ^ "GIMPS Discovers 48th Mersenne Prime, 257,885,161-1 is now the Largest Known Prime". mersenne.org. Great Internet Mersenne Prime Search. 5 February 2013. Diakses tanggal 29 September 2017. 
  20. ^ a b "GIMPS Discovers 45th and 46th Mersenne Primes, 243,112,609-1 is now the Largest Known Prime". mersenne.org. Great Internet Mersenne Prime Search. 15 September 2008. Diakses tanggal 29 September 2017. 
  21. ^ "GIMPS Discovers 47th Mersenne Prime, 242,643,801-1 is newest, but not the largest, known Mersenne Prime". mersenne.org. Great Internet Mersenne Prime Search. 12 April 2009. Diakses tanggal 29 September 2017. 
  22. ^ "GIMPS Discovers 44th Mersenne Prime, 232,582,657-1 is now the Largest Known Prime". mersenne.org. Great Internet Mersenne Prime Search. 11 September 2006. Diakses tanggal 29 September 2017. 
  23. ^ "PrimeGrid's Seventeen or Bust Subproject" (PDF). primegrid.com. PrimeGrid. Diakses tanggal 30 September 2017. 
  24. ^ "GIMPS Discovers 43rd Mersenne Prime, 230,402,457-1 is now the Largest Known Prime". mersenne.org. Great Internet Mersenne Prime Search. 24 December 2005. Diakses tanggal 29 September 2017. 
  25. ^ "GIMPS Discovers 42nd Mersenne Prime, 225,964,951-1 is now the Largest Known Prime". mersenne.org. Great Internet Mersenne Prime Search. 27 February 2005. Diakses tanggal 29 September 2017. 
  26. ^ "GIMPS Discovers 41st Mersenne Prime, 224,036,583-1 is now the Largest Known Prime". mersenne.org. Great Internet Mersenne Prime Search. 28 May 2004. Diakses tanggal 29 September 2017. 
  27. ^ "GIMPS Discovers 40th Mersenne Prime, 220,996,011-1 is now the Largest Known Prime". mersenne.org. Great Internet Mersenne Prime Search. 2 December 2003. Diakses tanggal 29 September 2017. 
  28. ^ "PrimeGrid's Generalized Fermat Prime Search" (PDF). primegrid.com. PrimeGrid. Diakses tanggal 7 November 2018. 
  29. ^ "PrimeGrid's Generalized Fermat Prime Search" (PDF). primegrid.com. PrimeGrid. Diakses tanggal 30 September 2017. 
  30. ^ "PrimeGrid's Prime Sierpinski Problem" (PDF). primegrid.com. PrimeGrid. Diakses tanggal 29 September 2017. 
  31. ^ "PrimePage Primes: 7 x 2^18233956 + 1". Diakses tanggal 10 February 2021. 
  32. ^ "The Prime Database: 3*2^17748034-1". primes.utm.edu. The Prime Pages. Diakses tanggal 13 September 2021. 

Pranala luar

sunting
Diperoleh dari "https://id.wikipedia.org/w/index.php?title=Bilangan_prima_terbesar_yang_diketahui&oldid=21980313"