Berkas:Prime number theorem ratio convergence.svg
Ukuran pratayang PNG ini dari berkas SVG ini: 250 × 160 piksel Resolusi lainnya: 320 × 205 piksel | 640 × 410 piksel | 1.024 × 655 piksel | 1.280 × 819 piksel | 2.560 × 1.638 piksel.
Ukuran asli (Berkas SVG, secara nominal 250 × 160 piksel, besar berkas: 87 KB)
Riwayat berkas
Klik pada tanggal/waktu untuk melihat berkas ini pada saat tersebut.
| Tanggal/Waktu | Miniatur | Dimensi | Pengguna | Komentar | |
|---|---|---|---|---|---|
| terkini | 21 Maret 2013 13.07 |  | 250 × 160 (87 KB) | Dcoetzee | Change n to x to match article |
| 21 Maret 2013 12.30 |  | 250 × 160 (86 KB) | Dcoetzee | Convert formula from graphics to pure SVG using http://www.tlhiv.org/ltxpreview/ | |
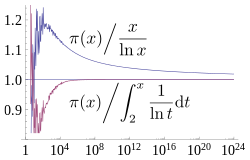
| 21 Maret 2013 12.23 |  | 250 × 160 (130 KB) | Dcoetzee | {{Information |Description ={{en|1=A plot showing how two estimates described by the prime number theorem, <math>\frac{n}{\ln n}</math> and <math>\int_2^n \frac{1}{\ln t} \mathrm{d}t = Li(n) = li(n) - li(2)</math> converge asymptotically towards <ma... |
Penggunaan berkas
2 halaman berikut menggunakan berkas ini:
Penggunaan berkas global
Wiki lain berikut menggunakan berkas ini:
- Penggunaan pada ar.wikipedia.org
- Penggunaan pada bn.wikipedia.org
- Penggunaan pada ca.wikipedia.org
- Penggunaan pada el.wikipedia.org
- Penggunaan pada en.wikipedia.org
- Penggunaan pada fa.wikipedia.org
- Penggunaan pada gl.wikipedia.org
- Penggunaan pada he.wikipedia.org
- Penggunaan pada hu.wikipedia.org
- Penggunaan pada hy.wikipedia.org
- Penggunaan pada ja.wikipedia.org
- Penggunaan pada mk.wikipedia.org
- Penggunaan pada no.wikipedia.org
- Penggunaan pada pl.wikipedia.org
- Penggunaan pada sl.wikipedia.org
- Penggunaan pada sr.wikipedia.org
- Penggunaan pada sv.wikipedia.org
- Penggunaan pada ta.wikipedia.org
- Penggunaan pada vi.wikipedia.org



